티스토리 뷰
안녕하세요! Ick입니다.
오늘은 가중치가 음수가 아닌 그래프에서 하나의 노드로부터 다른 노드들까지의 최단거리를 알 수 있는
다익스트라 알고리즘에 대해 알아보려고합니다.
다익스트라 알고리즘을 그냥 있는 그대로 나타내는 방법과 우선순위 큐를 사용하는 방법이 있는데요...
저는 우선순위 큐를 사용한 다익스트라 알고리즘을 이해하는데 정말 오래 걸렸습니다.ㅠ,ㅠ
그래서 다신 까먹지 않기 위해 글을 써보려고 합니다!
다익스트라 알고리즘 - Dijkstra
우선 다익스트라 알고리즘은 간선의 음수인 가중치가 없는 그래프에서만 사용할 수 있습니다.
여기서 방향 그래프, 무방향 그래프는 상관이 없습니다.
또한 하나의 노드에서 다른 모든 노드의 최단거리를 구하는 알고리즘이란 것을 기억해야 합니다!!
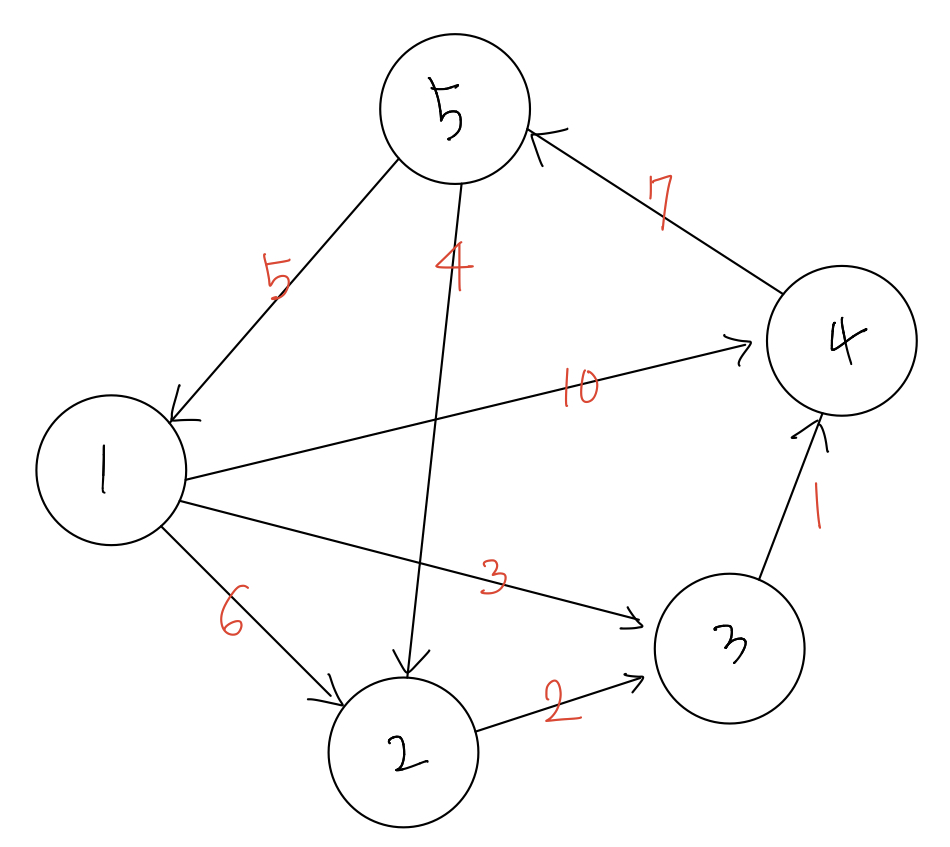
위의 그래프로 다익스트라를 이해해 보겠습니다.
위의 그래프는 방향이 있는 그래프입니다.
우선 정점은 5개이고 간선은 8개입니다.
간선의 가중치는 제가 빨간색으로 적었어요.
예를 들어 1번 정점에서 4번 정점으로 가는 방법은 몇 가지 있을까요?
1 -> 2 -> 3 -> 4 , 가중치 합 : 9
1 -> 3 -> 4 , 가중치 합 : 4
1 -> 4 , 가중치 합 : 10
정도가 있겠네요!
하지만 가중치가 가장 작은 경로는 1 -> 3 -> 4 라는 것을 알 수 있습니다.
이렇게 하나의 정점에서 다른 모든 정점으로 갈 때 가중치가 가장 적은 경로로 가는 방법을 찾는 것이 다익스트라입니다.
그럼 한 번 같이 다익스트라로 1번 정점에서 다른 정점으로 가는 방법 중 가중치가 가장 작은 방법을 찾아볼까요?
우선 이 그래프의 가중치 테이블을 만들어 보겠습니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 10 | 무한 |
| 정점 2 | 무한 | 0 | 2 | 무한 | 무한 |
| 정점 3 | 무한 | 무한 | 0 | 1 | 무한 |
| 정점 4 | 무한 | 무한 | 무한 | 0 | 7 |
| 정점 5 | 5 | 4 | 무한 | 무한 | 0 |
위와 같이 테이블을 만들 수 있습니다.
자기 자신으로 가는 가중치는 0으로 설정하고 한 번만에 갈 수 없는 경우 무한으로 설정해줬어요.
여기서 저희가 알고 싶은 것은 정점 1에서부터 다른 정점까지의 최단 거리이므로
아래와 같이 결과를 저장할 테이블을 하나 준비해줍니다.
이때 자기 자신으로 가는 가중치는 0으로 만들어줘야 합니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 무한 | 무한 | 무한 | 무한 |
그럼 이제 차근차근 해보겠습니다.
우선 현재 정점 1에서 다른 정점으로 갈 때 가중치가 가장 작은 값에서부터 시작해보겠습니다.
당연하겠지만 자기 자신으로 가는 가중치가 0이므로 가장 작습니다.
정점 1은 (1 -> 2, 가중치 6), (1 -> 3, 가중치 3), (1 -> 4, 가중치 10) 간선을 가지고 있습니다.
현재 1 -> 2로 가는 가중치는 무한인데 6이 무한보다 작기 때문에 무한을 6으로 수정합니다.
같은 방법으로 나머지 간선들도 처리해 주면 테이블이 다음과 같이 수정됩니다.
체크한 부분은 노란색으로 칠하도록 하겠습니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 10 | 무한 |
그다음 작은 값은 어디일까요?
정점 1에서 정점 3으로 가는 가중치가 3으로 다음으로 작으니 여기를 체크해보겠습니다.
정점 3은 (3 -> 4, 가중치 1) 간선 밖에 없네요.
그럼 현재 1 -> 4로 바로 가는 가중치는 10인데 1 -> 3 -> 4로 가게 되면 3 + 1 = 4로 더 작아집니다.
바로 수정을 해주면 되는 것이죠!
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 4 | 무한 |
다음으로 가중치가 작은 것은 정점 1에서 정점 4로 갈 때입니다.
정점 4는 (4 -> 5, 가중치 7) 간선이 있습니다.
즉 정점 1에서 정점 5로 갈 때 정점 4를 거쳐가면 가중치는 4 + 7 = 11가 됩니다.
현재 정점 1에서 정점 5로 바로 가는 가중치는 무한이므로 11이 더 작기 때문에 수정해줍니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 4 | 11 |
다음은 정점 1 -> 정점 2로 가는 가중치가 작습니다.
정점 2는 (2 -> 3, 가중치 2) 간선이 있네요
현재 1 -> 3의 가중치는 3인데 2를 거쳐가면 6 + 2 = 8 이므로 바꾸면 오히려 손해입니다.
따라서 그냥 넘어가도록 하겠습니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 4 | 11 |
드디어 하나밖에 남지 않았습니다.
정점 5는 (5 -> 1, 가중치 5), (5 -> 2, 가중치 2) 간선이 있습니다.
현재 1 ->1 가중치는 0이므로 수정할 필요가 없고
1 -> 2로 가는 가중치는 6입니다.
1 -> 5 -> 2로 가는 가중치는 11 + 2 = 13 이므로 바꾸면 손해입니다.
따라서 그냥 넘어가면 됩니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 4 | 11 |
위의 테이블이 정점 1에서 각 정점들로 가는 최소 가중치입니다.
지금 본 방법은 출발 정점에서 모든 정점으로 가는 경우를 모두 확인한 것입니다.
함께 해보셔서 아시겠지만 1,2,3,4,5 정점 모두를 확인했었죠?
하지만 이 방법은 정점만 엄청나게 많고 간선이 없을 경우엔 너무나도 불필요한 연산을 반복하게 됩니다.
예를 들어 극단적으로 정점은 100만 개인데 간선은 1개인 예가 있습니다.
실제로 테이블에서 수정할 수 있는 값은 연결된 정점 하나일 텐데 정점이 100만 개이기 때문에
100만 번 * 100만 번을 확인해야 하는 것입니다.
시간 복잡도는 O(N^2)입니다.
이 때문에 실제론 위와 같은 방법보다는 간선을 중심으로 확인합니다.
이것이 제가 이해하기 힘들었던 우선순위 큐를 사용하는 방법입니다.
우선순위 큐를 사용한 다익스트라
우선순위 큐는 힙을 사용하기 때문에 항상 루트 노드에 최솟값이나 최댓값이 저장되어 있습니다.
따라서 늘 간선 중 가장 작은 값부터 고려하게 해 줍니다.

이 그래프로 다시 예를 들어 보겠습니다.
우선 결과를 저장할 테이블은 동일하게 만들어 줘야 합니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 무한 | 무한 | 무한 | 무한 |
그리고 우선순위 큐에는 출발 정점이 자기 자신으로 가는 데이터를 넣어주고
알고리즘을 시작하면 됩니다.

위와 같이 말이죠!
그런 뒤 방금 넣어준 데이터를 꺼내 도착 정점을 확인하고 도착 정점에 연결된 간선들을 확인합니다.
지금은 도착 정점이 1이니까 간선들은 (1 -> 2, 가중치 6), (1 -> 3, 가중치 3), (1 -> 4, 가중치 10) 이렇게 3개가 있겠네요!
비교하여 정답 테이블을 수정하는 부분은 동일합니다.
다시 해보면 현재 1->2의 가중치는 무한입니다.
따라서 현재 확인 중인 간선인 (1 -> 2, 가중치 6)를 사용하는 것이 더 이득이죠.
따라서 수정해줍니다.
아까는 여기서 다음 간선으로 넘어갔지만 이번에는 우선순위 큐에 넣어주고 넘어가면 됩니다.
나머지 간선들도 확인 후 수정이 된다면 우선순위 큐에 넣어주면 됩니다.
여기서 우선순위 큐에 넣어줄 때 가중치는 수정된 값을 넣어주셔야 하고 정점 정보에는 도착 정점을 넣어주셔야 합니다.
즉 지금 경우엔 도착 정점은 2, 수정되려는 값은 0 + 6입니다.
따라서 우선순위 큐에는 (2,6)의 모양을 넣어주시면 됩니다!
지금 확인해야 할 간선들을 모두 확인하면 테이블은 아래와 같이 수정되겠죠?
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 10 | 무한 |
1번 정점에 연결된 모든 간선을 체크하면 아래와 같이 우선순위 큐가 되어있을 거예요.

위와 같이 현재 가중치가 가장 작은 간선이 큐의 루트 노드 역할을 하고 있을 거예요.
저희는 얘를 다시 뽑아서 아까 한 작업을 반복해주시면 됩니다.
(3,3) 간선을 뽑아서 도착 정점인 정점 3에 연결된 간선을 확인해봅니다.
(3 -> 4, 가중치 1) 간선만 존재하네요~
현재 1 -> 4로 가는 가중치는 10입니다. 하지만 1 -> 3 -> 4로 가는 가중치는 3 + 1이므로 더 작네요
그럼 수정해줍니다.
도착 정점은 4번이고 수정되는 가중치 값은 4이므로 (4,4)를 큐에 넣어주시면 됩니다~
이렇게 계속 반복하다 큐에 더 이상 데이터가 존재하지 않을 때가 답입니다.
| 정점 1 | 정점 2 | 정점 3 | 정점 4 | 정점 5 | |
| 정점 1 | 0 | 6 | 3 | 4 | 11 |
물론 결과는 아까와 같습니다.
하지만 이 방법은 간선의 개수에 따라 반복 횟수가 변하므로 더 효율적입니다.
시간 복잡도는 O(N*logN)입니다.
이 글이 다익스트라를 이해하시는데 도움이 되시면 좋겠습니다..ㅠㅠ
감사합니다!!
'Algorithm > Basic' 카테고리의 다른 글
| [알고리즘] 크루스칼 알고리즘, 유니온 파인드 - Kruskal, Union Find [Swift] (0) | 2020.09.21 |
|---|---|
| [알고리즘] 힙 정렬 (Heap Sort) [Swift] (1) | 2020.09.13 |
| [알고리즘] 최소 비용 신장 트리 - Minimum Cost Spanning Tree (0) | 2020.08.31 |
- Total
- Today
- Yesterday
- Combine
- 테이블뷰
- 문법
- IOS
- Publisher
- document
- 앱개발
- BFS
- 코딩테스트
- pattern
- 스위프트
- operating
- dfs
- 아이폰
- mac
- Swift
- OSTEP
- OS
- DP
- operator
- 동시성
- 자료구조
- 알고리즘
- Apple
- 코테
- design
- 프로그래밍
- System
- Xcode
- 백준
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
