티스토리 뷰
안녕하세요! Ick입니다.
최소 비용 신장 트리 - Minimum Cost Spanning Tree
오늘은 여러 알고리즘 중에서 최소 비용 신장 트리라고 불리는 알고리즘에 대해 알아보려고 합니다!
최소 비용 신장 트리, 최소 스패닝 트리라고 불리는 이 알고리즘은 가중치 무방향 그래프에서 모든 정점을 연결할 때 최소의 비용으로 연결할 수 있는 방법을 찾는 알고리즘입니다.
가중치 무방향 그래프는 무엇일까요?
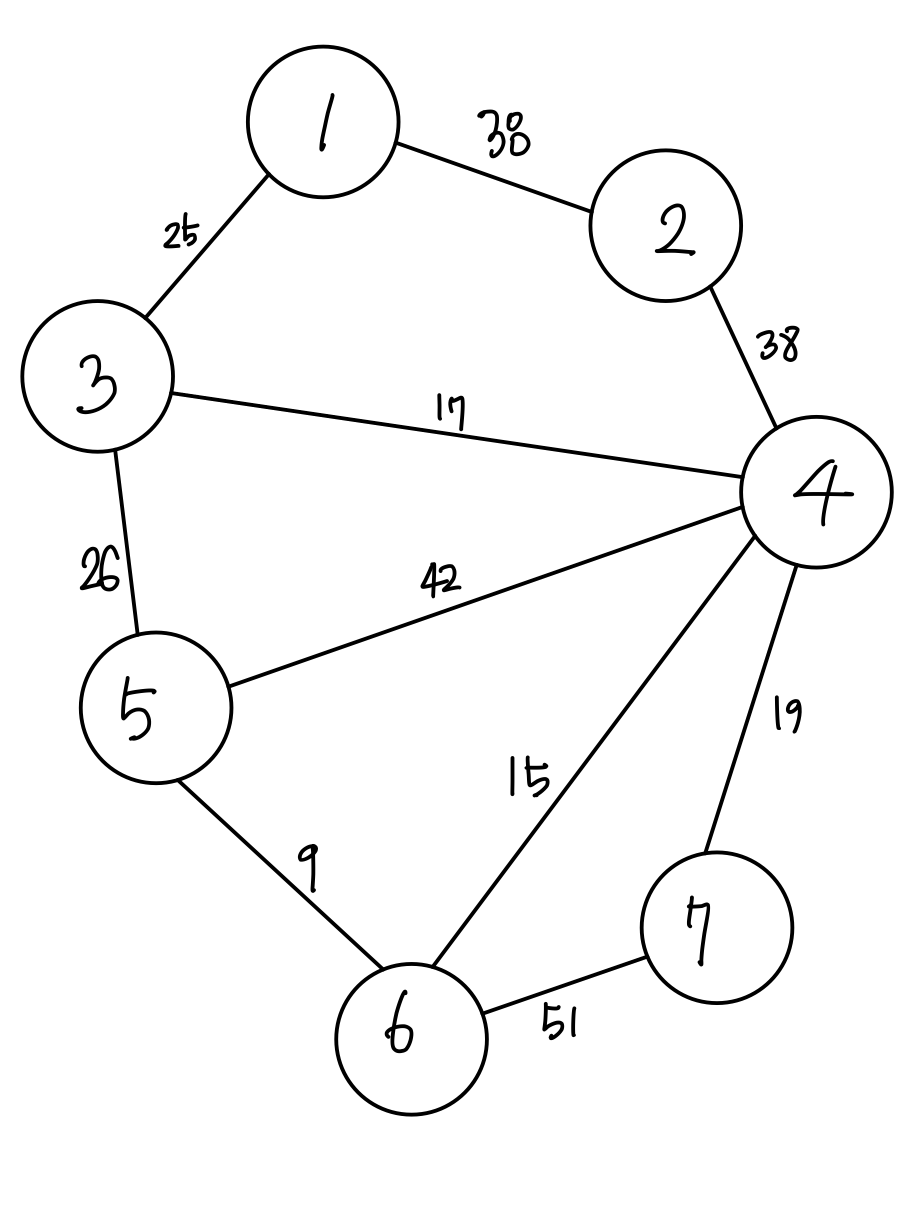
위와 같이 그래프가 있을 때 정점 사이에 가중치가 있고 간선에 방향이 없는 그래프를 가중치 무방향 그래프라고 합니다.
예를 들어 위의 그래프에서 정점 1에서 정점 3으로 가고 싶다면 25의 가중치를 가진 간선을 사용하면 되는 것입니다.
이번 글에서 배울 최소 비용 신장 트리는 이러한 그래프에서 모든 정점을 최소의 비용으로 연결하는 방법입니다.
단 모든 정점을 연결할 때 사이클을 형성하지 않아야 합니다.
여기서 사이클이란!
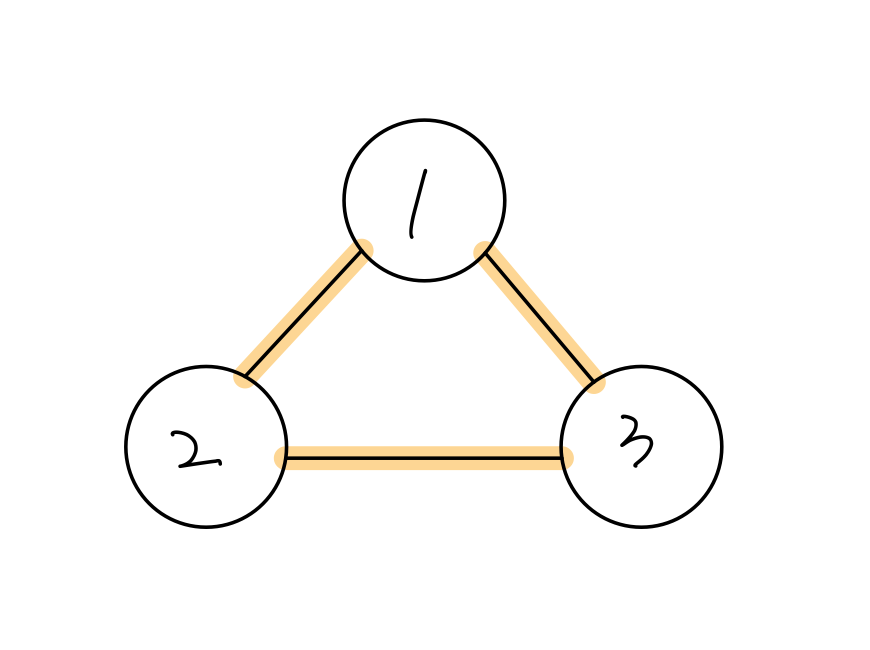
위의 그림과 같이 간선들을 선택한 경우가 사이클이 발생하게 된 경우입니다.
위의 그림에서 간선 하나를 제외하더라도 3개의 정점은 연결된 상태이므로 최소의 비용을 고려하는 이 알고리즘에서 사이클의 존재는 비효율적인 것이죠!
이 때문에 간선의 수는 (정점 - 1)개 만큼만 존재할 때 정답이 될 수 있습니다.
그럼 우선 위의 그래프에서 최소 비용 신장트리는 어떤 모양일까요?
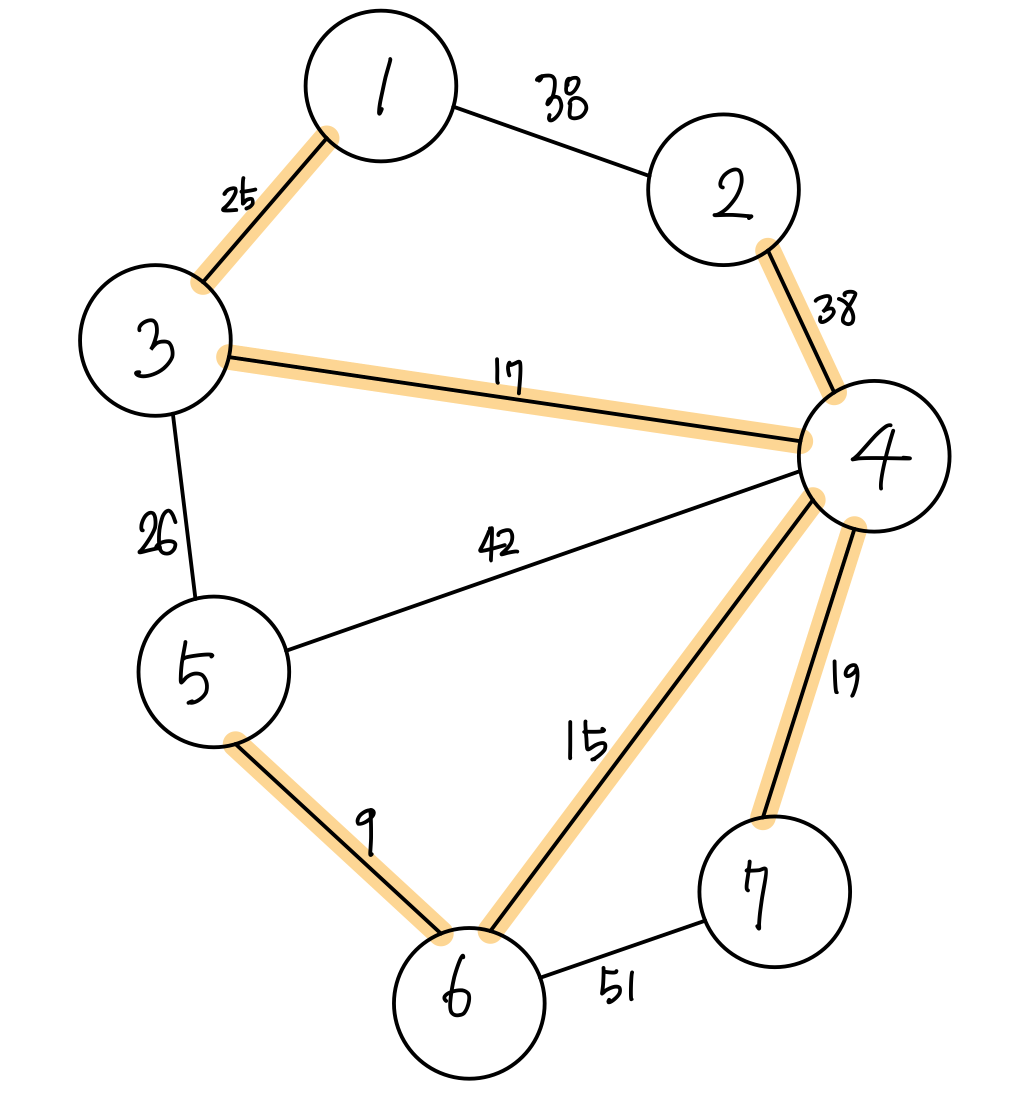
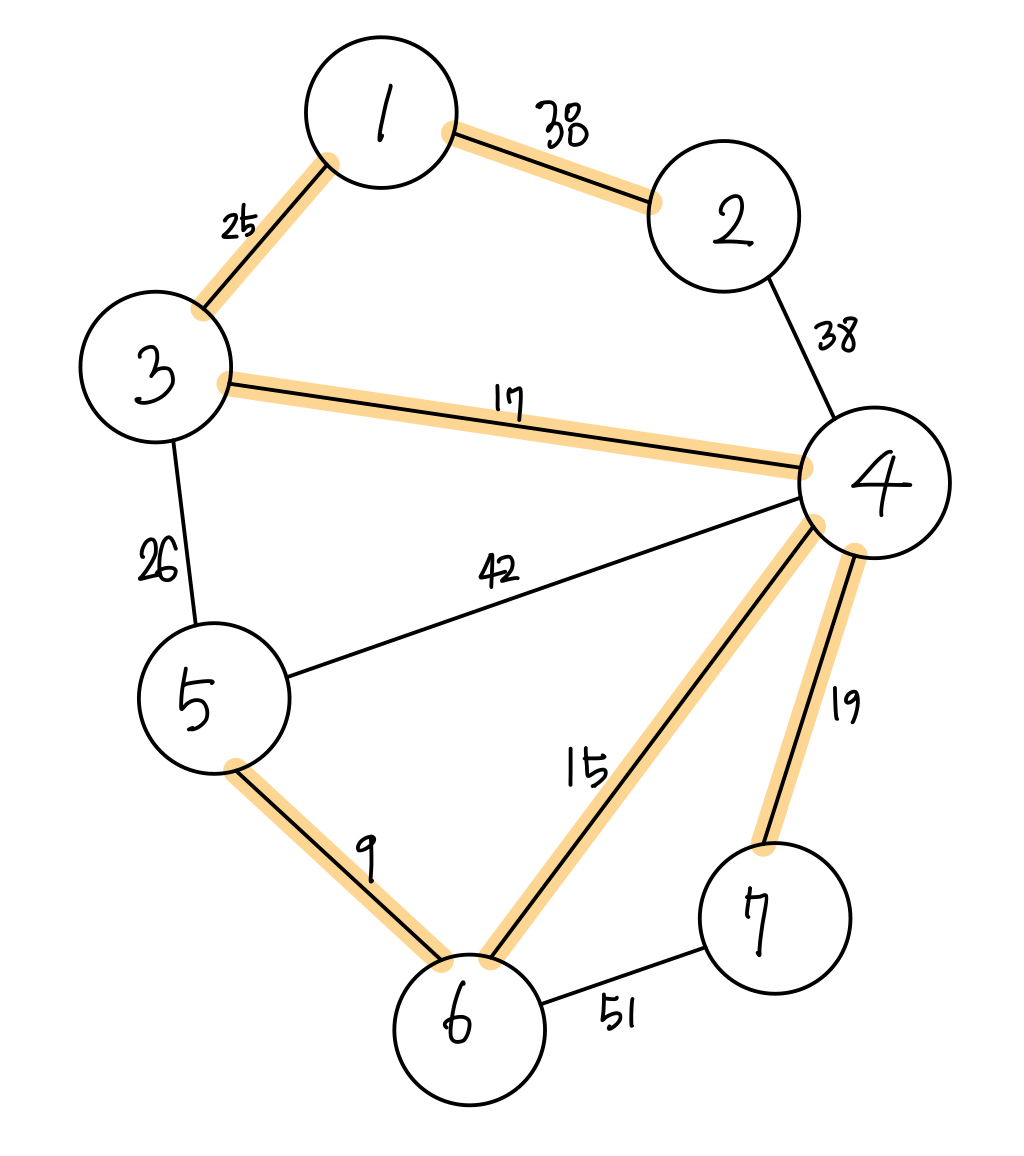
위와 같이 2개의 트리가 모두 정답이 될 수 있습니다.
여기서 알 수 있는 점은 어떠한 가중치 무방향 그래프에서 최소비용 신장 트리는 여러 개 존재할 수 있다는 점입니다.
그럼 이젠 이러한 정답을 얻기 위해 어떤 방식으로 진행하는지 알아보겠습니다.
최소 비용 신장 트리 알고리즘엔 Kruskal(크루스칼) 알고리즘, Prim(프림) 알고리즘이 가장 유명합니다.
그럼 두 알고리즘을 알아볼까요?
Kruskal (크루스칼) 알고리즘
먼저 Kruskal 알고리즘을 살펴보도록 하겠습니다.
크루스칼 알고리즘은 간선을 기준으로 트리를 만드는 방법입니다.
간선을 기준으로 한다는 것은 간선의 가중치를 기준으로 하는 것인데 가중치가 작은 간선부터 트리에 추가하겠다는 말입니다.
아까 본 그래프를 사용해서 방법을 이해해 보겠습니다.
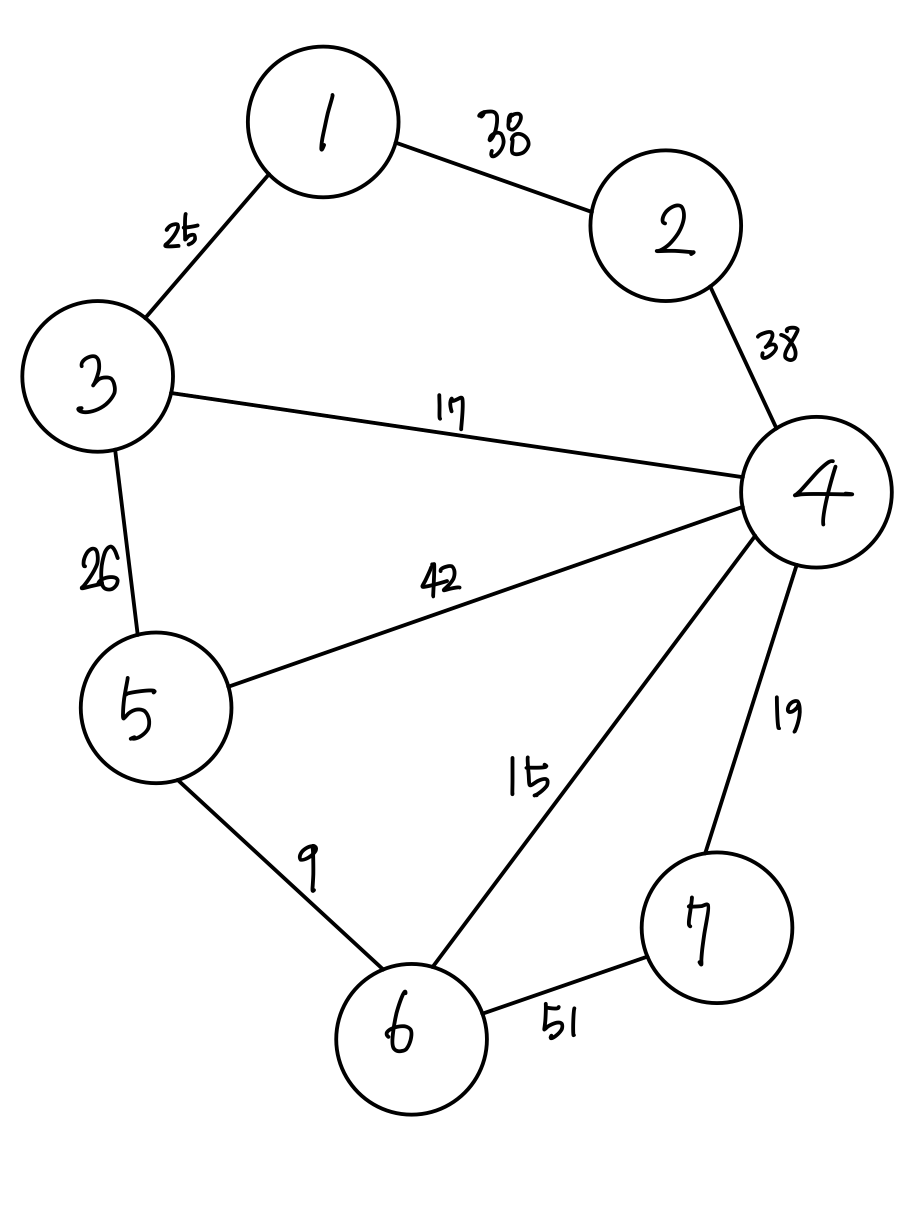
위의 그림에서 간선들의 가중치는 [ 25, 38, 17, 38, 26, 42, 9, 15, 19, 51 ] 입니다.
이 가중치들을 크기 순으로 정렬하면 [ 9, 15, 17, 19, 25, 26, 38, 38, 51 ] 입니다.
따라서 가중치가 9인 간선부터 트리에 추가하는 것입니다.
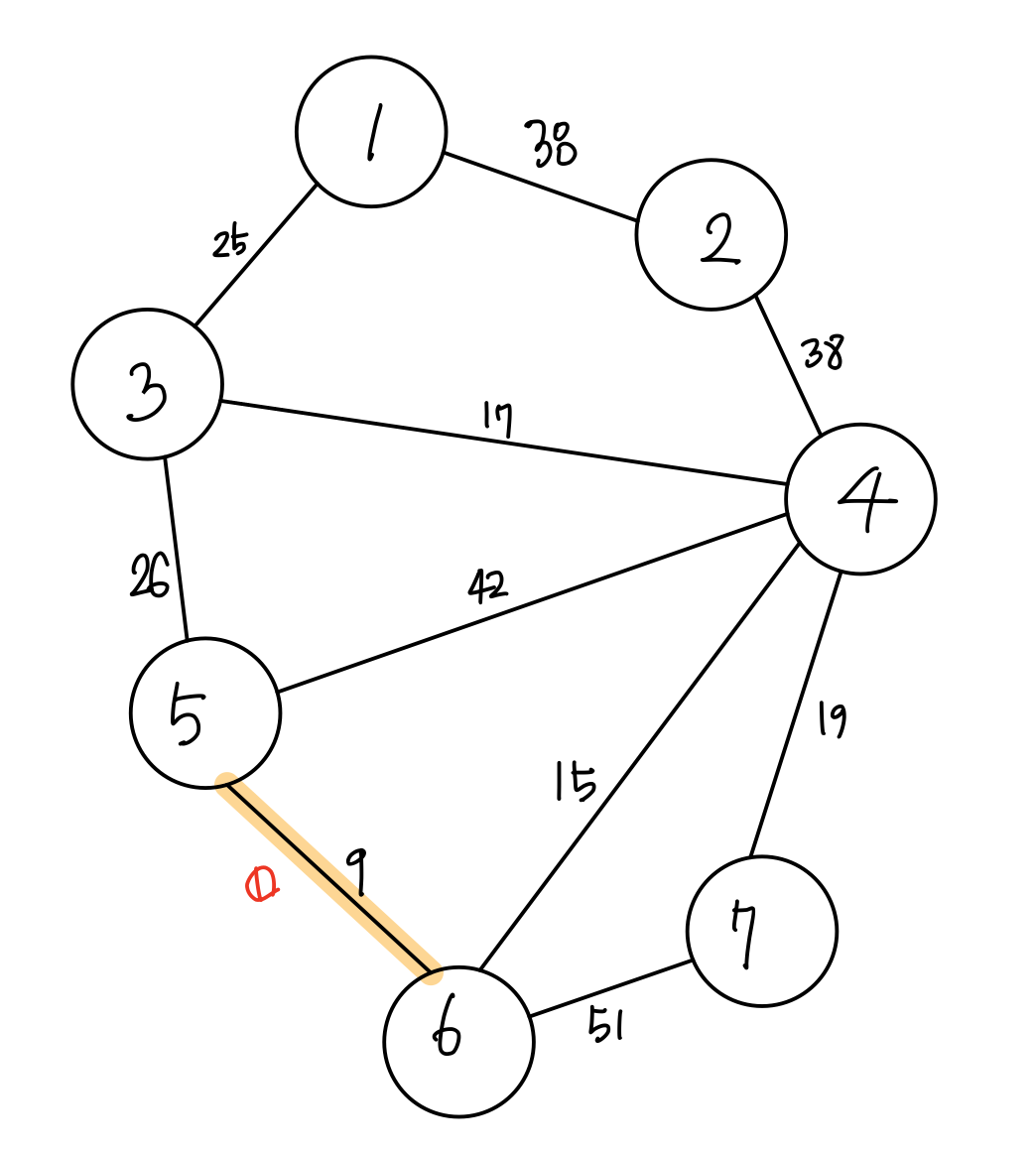
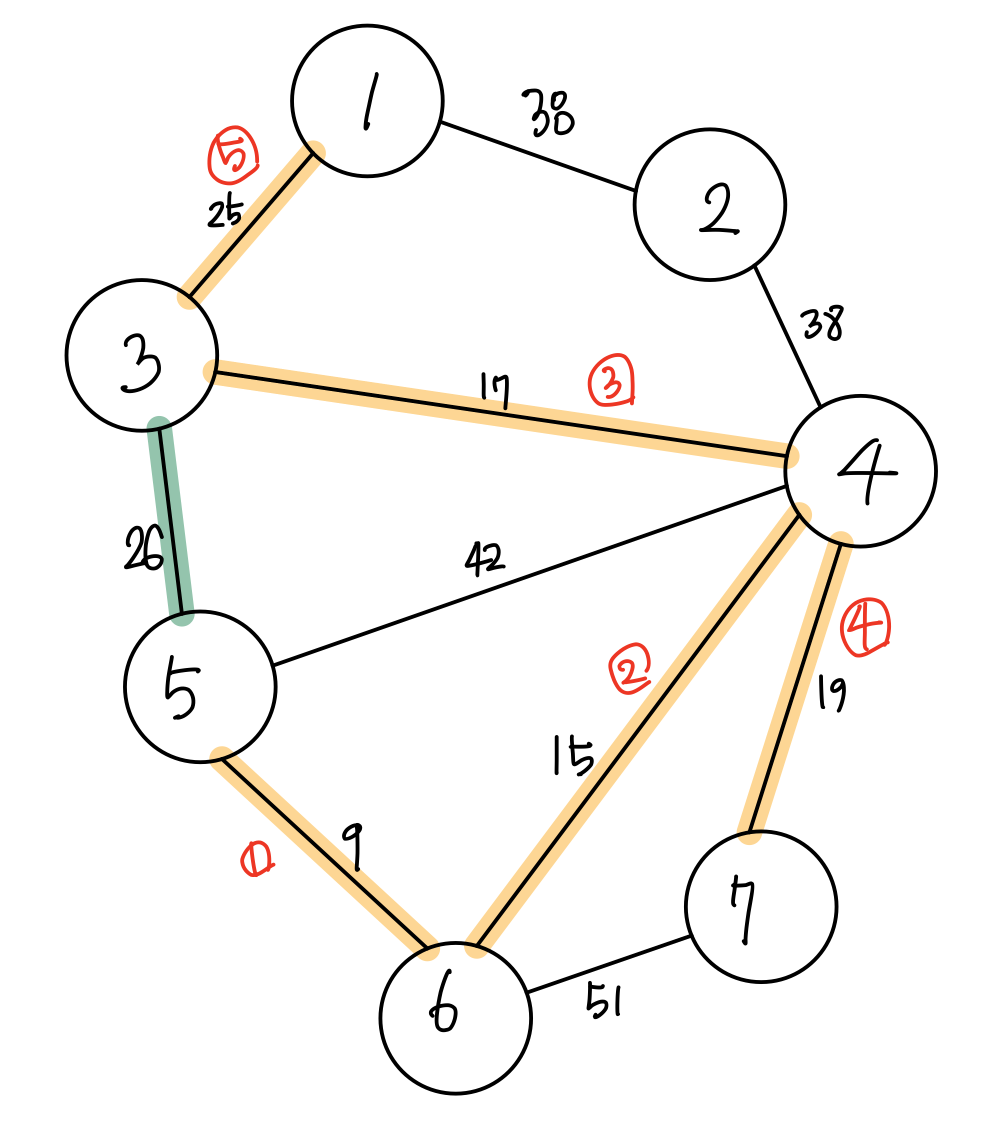
그다음은 15를 추가하고, 17, 19, 25를 추가합니다. 그러다 26을 추가하려고 할 때 문제가 발생합니다.
위의 그림에서 26 가중치를 가진 간선은 초록색으로 표시했습니다.
이때 만약 26 가중치를 가진 간선을 추가하게 되면 사이클이 발생하게 됩니다.
최소비용 신장 트리에서는 이런 사이클이 없어야 하기 때문에 26은 추가할 수 없습니다.
따라서 그다음 작은 38 가중치를 가진 간선을 고려하는데 여기선 두 개가 있고 두 개 모두를 추가하면 사이클이 발생하므로 한 개만 추가할 수 있습니다.
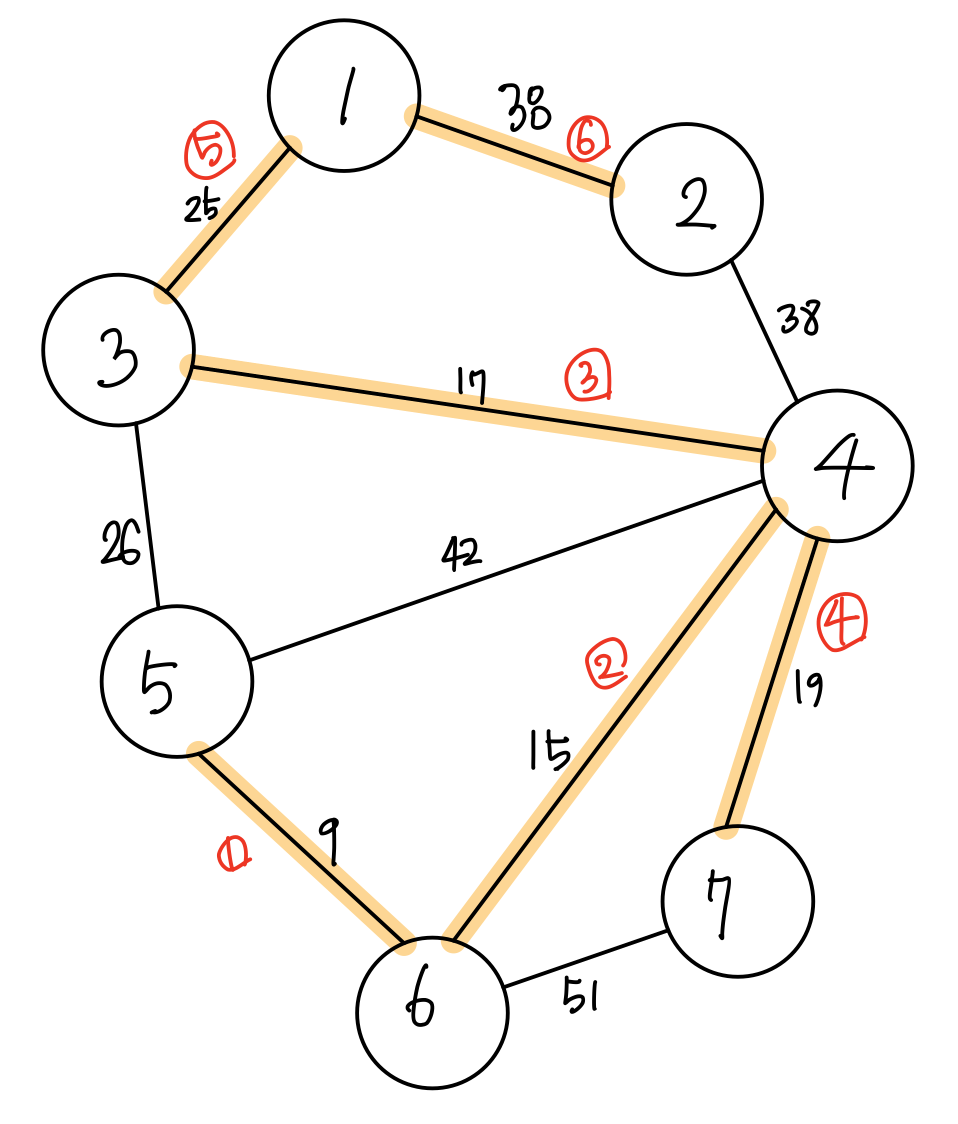
그렇게 하면 간선의 수가 6개가 되고 그래프의 정점보다 1 작게 되므로 위와 같은 그래프가 정답이 됩니다.
Prim (프림) 알고리즘
아까 본 크루스칼 알고리즘은 간선을 중심으로 트리를 구성했다면 프림 알고리즘은 정점을 기준으로 트리를 구성하는 방법입니다.
다시 처음 그래프를 가져와 보겠습니다.
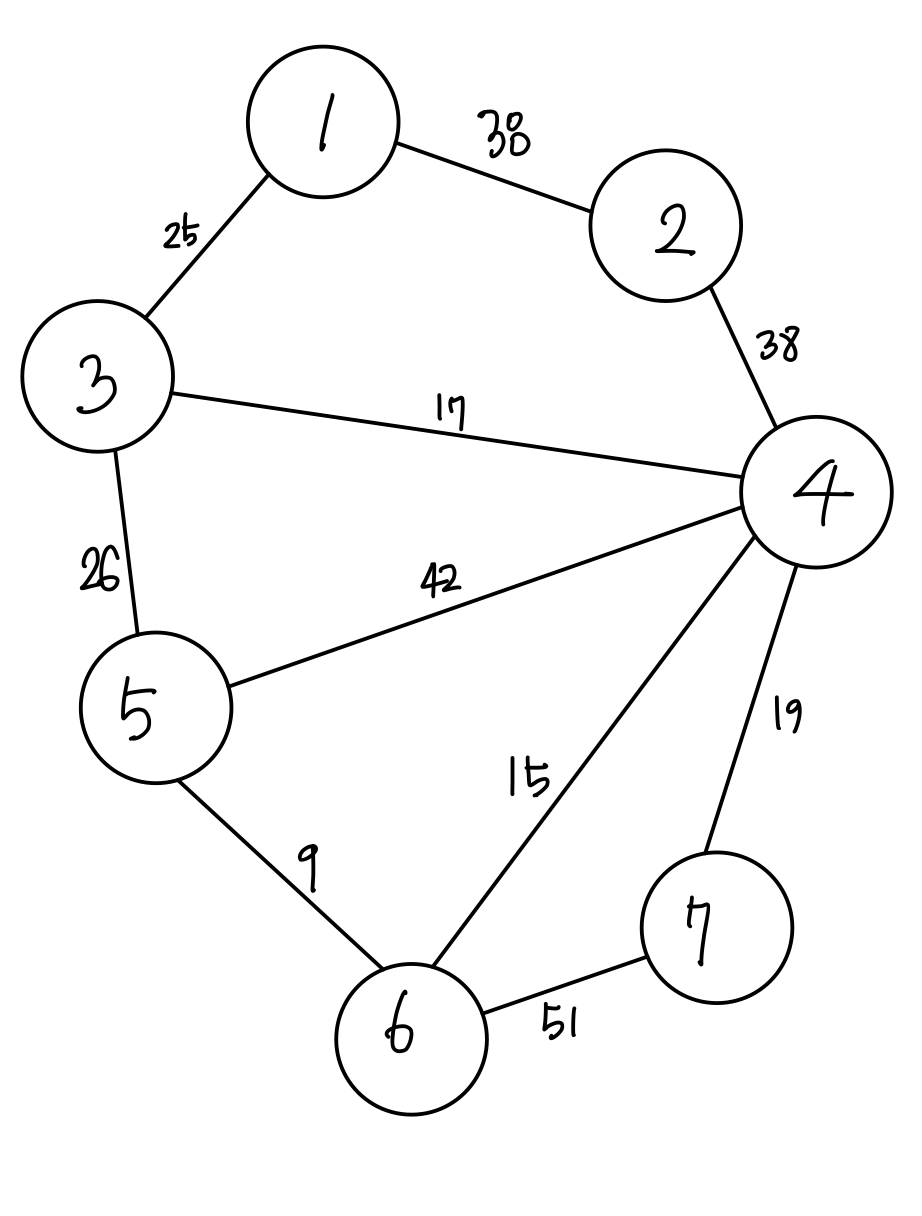
정점을 기준으로 트리를 구성한다는 말을 이해해 보겠습니다.
먼저 시작 정점을 임의로 정합니다. 저는 정점 1에서 시작해보겠습니다.
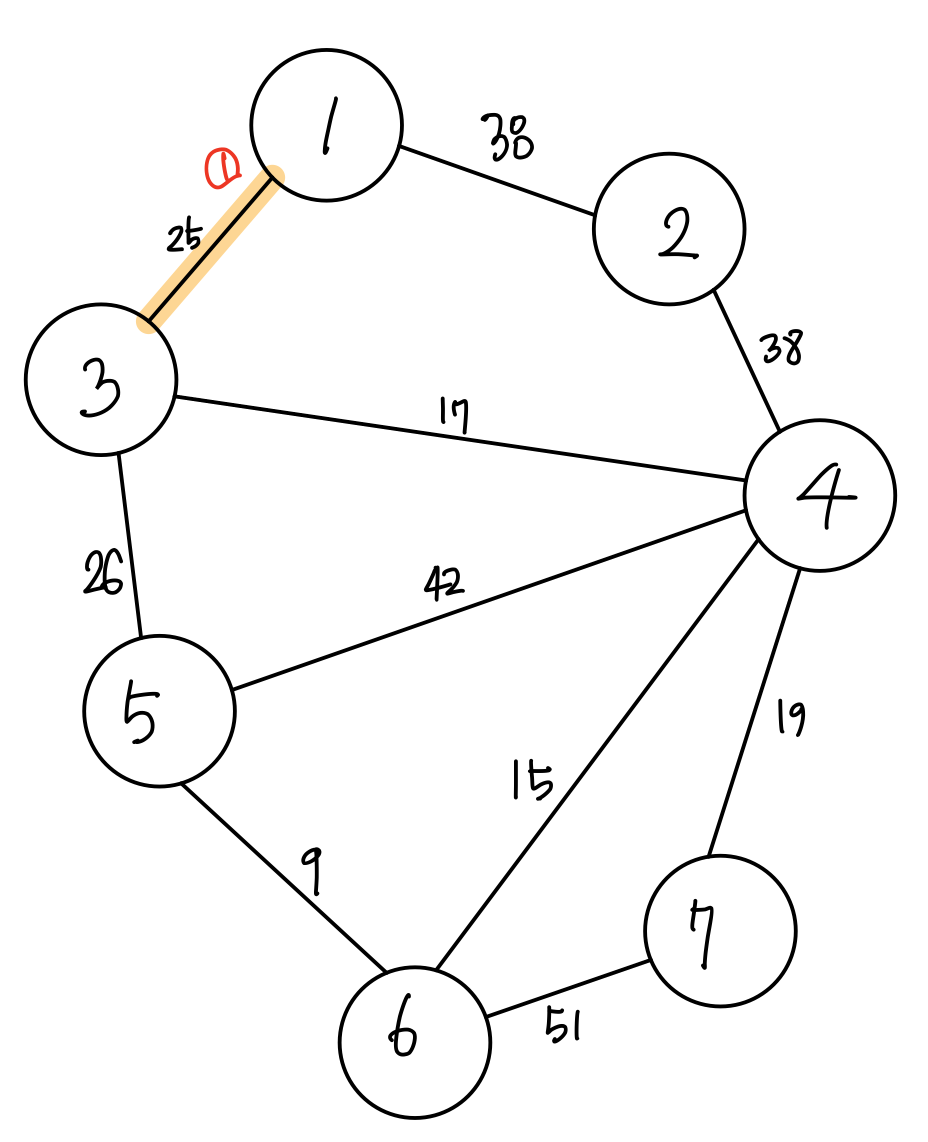
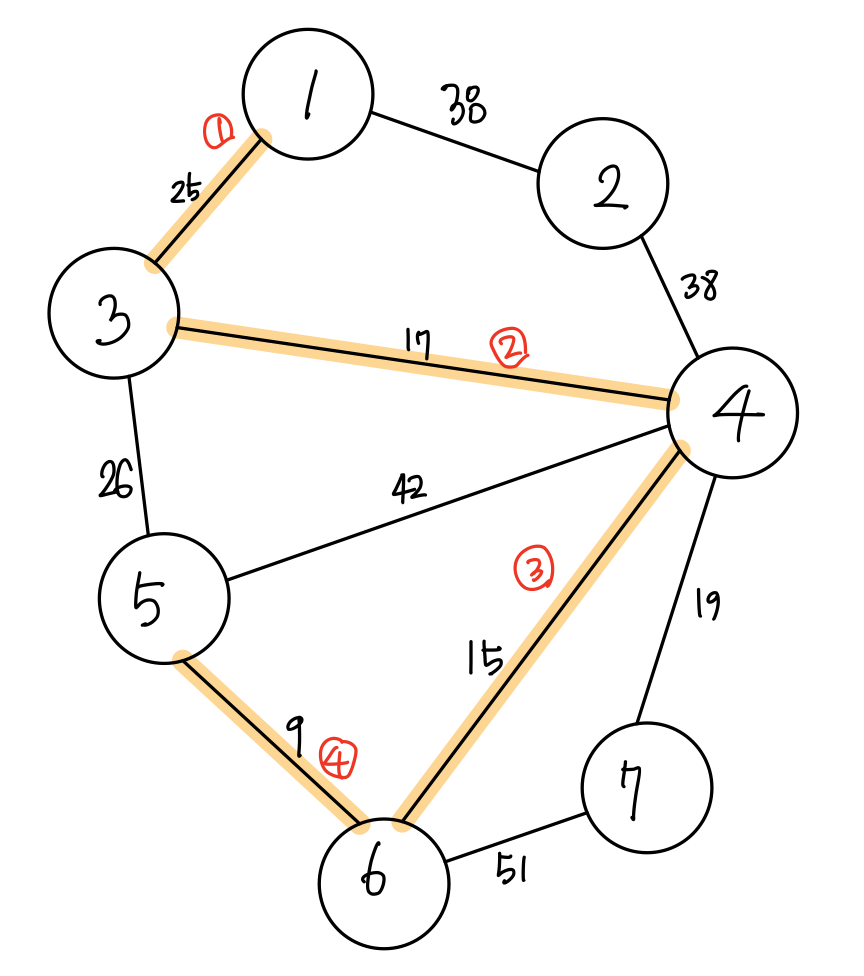
먼저 정점 1에는 25, 38 가중치를 가진 간선들이 있고 여기서 작은 간선을 선택합니다.
그렇게 도착한 정점 3에는 17, 25, 26 가중치를 가진 간선들이 있습니다. 가장 작은 17 가중치를 가진 간선을 선택하고 정점 5에 갈 때까지 동일하게 반복합니다.
정점 5에 도착하면 연결된 어떤 간선을 선택해도 사이클이 발생하게 됩니다.
따라서 현재 선택되지 않은 정점을 임의로 선택해 다시 진행합니다.
예를 들어 정점 7을 선택한 뒤 동일하게 반복하면 다음 결과가 나올 거예요.
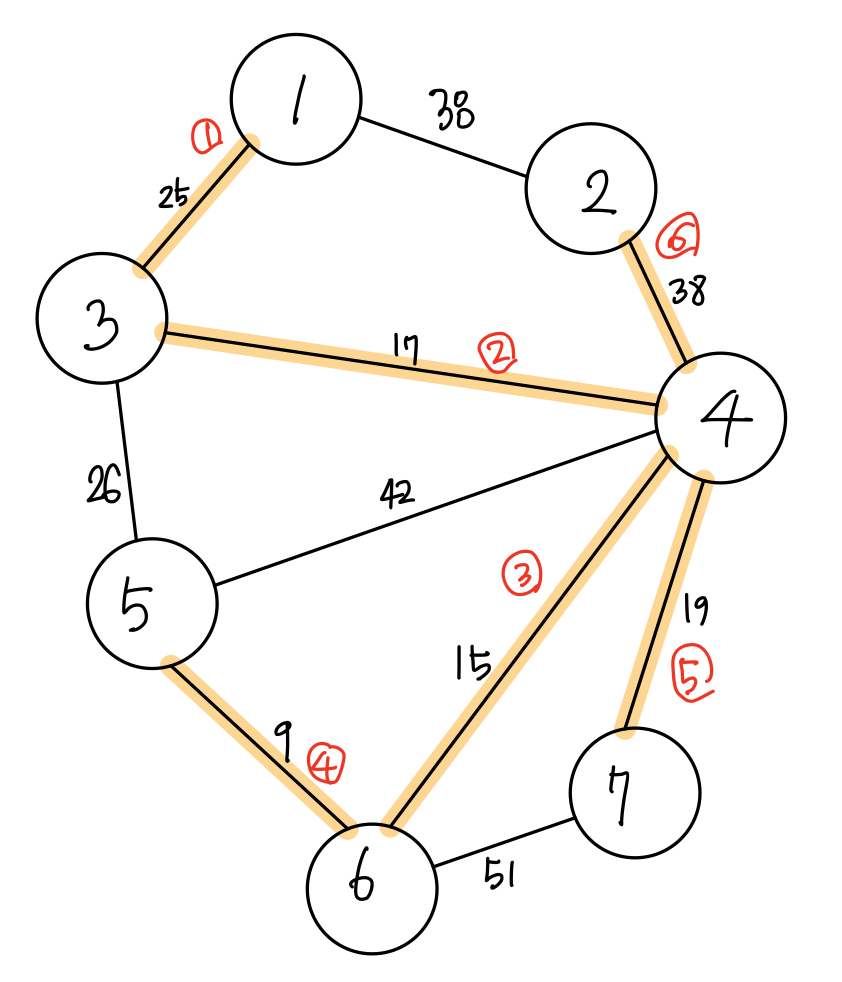
이렇게 최소비용 신장 트리를 찾을 수 있습니다.
실제 코드로 구현하는 방법은 아래 링크를 확인해주세요!
프림 알고리즘
감사합니다~
'Algorithm > Basic' 카테고리의 다른 글
| [알고리즘] 크루스칼 알고리즘, 유니온 파인드 - Kruskal, Union Find [Swift] (0) | 2020.09.21 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 - Dijkstra (0) | 2020.09.15 |
| [알고리즘] 힙 정렬 (Heap Sort) [Swift] (1) | 2020.09.13 |
- Total
- Today
- Yesterday
- dfs
- OS
- IOS
- 코테
- mac
- 프로그래밍
- 자료구조
- 앱개발
- document
- 스위프트
- DP
- Apple
- 문법
- 아이폰
- 백준
- pattern
- operator
- 동시성
- Swift
- design
- Combine
- System
- 코딩테스트
- 테이블뷰
- 알고리즘
- BFS
- operating
- OSTEP
- Publisher
- Xcode
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
