티스토리 뷰
안녕하세요 Ick입니다.
오늘은 여러 정렬 알고리즘 중 힙 정렬에 대해 공부했고 그에 대한 내용을 정리해볼까 합니다!
힙 정렬 (Heap Sort)
우선 정렬 알고리즘에는 버블 정렬, 병합 정렬, 퀵 정렬 등 여러 방법이 있는데요, 힙 정렬은 그중 시간 복잡도 O(N*logN)의 성능을 보이는 정렬 알고리즘입니다!
이러한 힙 정렬을 이해하기 위해선 힙(Heap)이라는 개념을 이해하셔야 합니다.
가장 중요한 것은 완전이진트리구조를 갖는다는 것입니다.
힙에는 최대 힙, 최소 힙이 있는데 최대 힙은 부모 노드가 자식 노드보다 값이 큰 힙을 말하며,
최소힙은 부모 노드가 자식 노드보다 값이 작은 힙을 말합니다.

그림으로 힙을 살펴보면 위와 같습니다. 최대 힙같은 경우엔 부모 노드가 자식 노드보다 커야 하므로 자연스럽게 루트 노드에는 트리에서 가장 큰 값이 담기게 됩니다. 최소 힙 같은 경우엔 부모 노드가 자식 노드보다 작아야 하므로 자연스럽게 루트 노드에는 트리에서 가장 작은 값이 담기는 것을 볼 수 있습니다.
힙 정렬에서는 이러한 힙의 구조로 되어있는 자료구조를 정렬하는 알고리즘이라고 볼 수 있습니다.
그 말은 먼저 정렬하고 싶은 자료구조를 힙 구조로 만들어야 한다는 말입니다!
그럼 같이 힙 구조로 만들고 정렬하는 방법을 살펴보겠습니다.

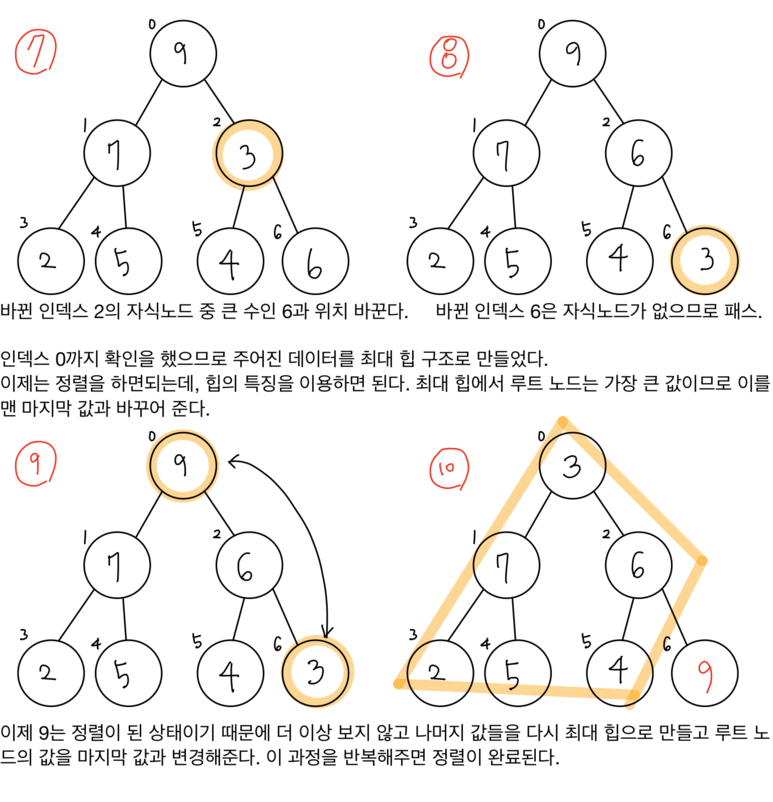
위의 그림의 1~8까지의 과정이 힙 구조로 만드는 과정이고 9~10 과정은 힙 구조로 만들어진 자료구조를 정렬하는 방법입니다.
물론 위의 예는 최대힙을 만드는 과정이었고 최소 힙을 만드는 과정은 크기 비교만 다를 뿐 동일합니다!
힙은 완전 이진 트리이기 때문에 전체 노드 수의 절반만 확인해줘도 모든 노드를 확인할 수 있습니다.
따라서 위의 경우 3번 인덱스부터 시작한 이유는 4,5,6 노드부터 확인해주는 것이 성능적으로 손해이기 때문입니다.
완전 이진 트리에서 자신의 자식 노드의 인덱스는 (자신의 인덱스 * 2) + 1, (자신의 인덱스 * 2) + 2 입니다.
즉 예를 들어 1번 인덱스의 자식 노드는 (1*2) + 1, (1*2) + 2 즉 3, 4번 노드입니다.
1~8 과정을 거쳐 자료구조를 힙 구조로 만들었다면 이제 정렬을 할 차례입니다.
9~10 과정이 정렬에 해당하는 과정입니다.
결과를 먼저 말씀드리면 위의 예에서는 최대 힙을 만들었기 때문에 정렬을 하고 아무런 작업을 해주지 않는다면 오름차순으로 결과가 나오게 됩니다.
그럼 정렬 과정을 살펴보겠습니다.
물론 최대 힙을 만들었다는 가정으로 진행하겠습니다!
9번에서 볼 수 있듯 루트 노드에는 최댓값이 저장되어 있습니다.
이를 마지막 노드와 위치를 바꿔주면 됩니다.
그리고 이렇게 바꾼 순간 마지막 노드는 정렬이 되었다고 보고 앞으로 신경 쓰지 않습니다.
그런 뒤 인덱스 0~인덱스 5까지 다시 힙 구조로 변경해줍니다.
그러면 다시 루트 노드에 가장 큰 값이 존재하게 되고 이를 다시 마지막 노드와 바꿔줍니다.
이 과정을 반복하면 정렬이 되게 됩니다.
요약하면 아래와 같습니다.
1. 자료구조를 힙구조로 만든다.
2. 루트 노드와 마지막 노드를 교체한다. 이 순간 마지막 노드는 정렬된 것이므로 더 이상 신경 쓰지 않는다.
3. 마지막 노드를 제외한 자료구조를 다시 힙 구조로 만든다.
4. 이 과정을 반복한다.
이해가 되셨나요???
그럼 이제 힙 정렬을 Swift로 구현해보겠습니다.
func myMaxHeapSort(_ list: [Int], reversed: Bool = false) -> [Int]{
var tempList = list
var result: [Int] = []
for i in stride(from: list.count-1, to:-1, by: -1){
if i == 0 {
guard let last = tempList.popLast() else { fatalError() }
result.append(last)
} else {
tempList = makeMaxHeap(tempList)
let temp = tempList[0]
tempList[0] = tempList[i]
tempList[i] = temp
guard let last = tempList.popLast() else { fatalError() }
result.append(last)
}
}
if reversed == false {
result.reverse()
return result
} else {
return result
}
}
func makeMaxHeap(_ list: [Int]) -> [Int]{
var result = list
for i in 1..<list.count{
var childNode = i
repeat{
let root: Int = (childNode - 1) / 2
if result[root] < result[childNode]{
let temp = result[childNode]
result[childNode] = result[root]
result[root] = temp
}
childNode = root
} while (childNode != 0)
}
return result
}
print(myMaxHeapSort(makeMaxHeap([3,5,4,2,7,9,6]),reversed: true))
'Algorithm > Basic' 카테고리의 다른 글
| [알고리즘] 크루스칼 알고리즘, 유니온 파인드 - Kruskal, Union Find [Swift] (0) | 2020.09.21 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 - Dijkstra (0) | 2020.09.15 |
| [알고리즘] 최소 비용 신장 트리 - Minimum Cost Spanning Tree (0) | 2020.08.31 |
- Total
- Today
- Yesterday
- Swift
- Combine
- 아이폰
- 스위프트
- 동시성
- dfs
- operator
- IOS
- 테이블뷰
- 코딩테스트
- mac
- pattern
- DP
- Apple
- operating
- 문법
- design
- 백준
- document
- 프로그래밍
- OSTEP
- System
- 앱개발
- 코테
- Publisher
- OS
- 자료구조
- 알고리즘
- BFS
- Xcode
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
