티스토리 뷰
문제 링크
13023번: ABCDE
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
www.acmicpc.net
문제
BOJ 알고리즘 캠프에는 총 N명이 참가하고 있다. 사람들은 0번부터 N-1번으로 번호가 매겨져 있고, 일부 사람들은 친구이다.
오늘은 다음과 같은 친구 관계를 가진 사람 A, B, C, D, E가 존재하는지 구해보려고 한다.
- A는 B와 친구다.
- B는 C와 친구다.
- C는 D와 친구다.
- D는 E와 친구다.
위와 같은 친구 관계가 존재하는지 안하는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 사람의 수 N (5 ≤ N ≤ 2000)과 친구 관계의 수 M (1 ≤ M ≤ 2000)이 주어진다.
둘째 줄부터 M개의 줄에는 정수 a와 b가 주어지며, a와 b가 친구라는 뜻이다. (0 ≤ a, b ≤ N-1, a ≠ b) 같은 친구 관계가 두 번 이상 주어지는 경우는 없다.
출력
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
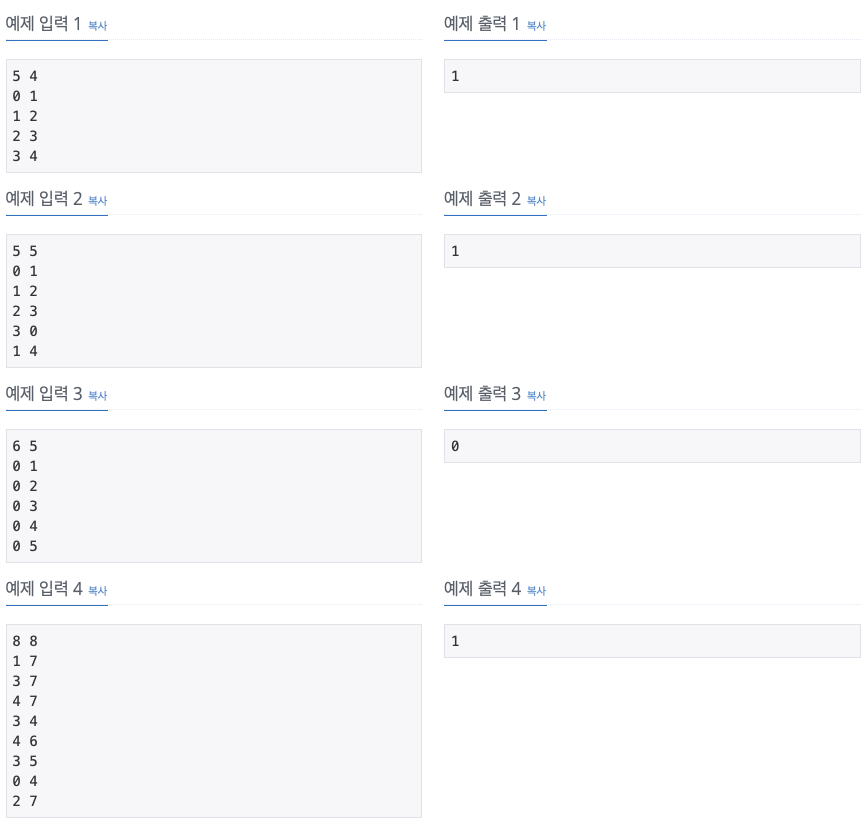
문제 풀이
이 문제는 주어지는 친구관계를 그래프로 만들어서 DFS로 처리해주면 되는 문제였습니다.
예를 들어 예제 1을 그래프로 만들어보면 아래와 같습니다.

문제에서 알아보고자 하는 조건은
- A는 B와 친구다.
- B는 C와 친구다.
- C는 D와 친구다.
- D는 E와 친구다.
이므로 위의 그림은 위의 조건을 만족하기 때문에 1을 출력하면 됩니다.

조건을 만족하지 않는 예를 살펴보기 위해서는 위와 같은 예를 보면 됩니다.
이러한 조건을 그래프의 관점에서 보면 4번 이상 방문하지 않은 노드에 방문 할 수 있는 경우를 찾아주면 되는 문제였습니다.
따라서 dfs를 수행 할 때 마다 레벨을 1씩 증가시켜 레벨이 4가 된다면 조건을 만족하는 것으로 처리해주면 문제를 해결할 수 있었습니다!
소스 코드
import Foundation
func solution() {
let firstLine = readLine()!.split(separator: " ").map({Int(String($0))!})
let n = firstLine[0], m = firstLine[1]
// 친구 관계 그래프
var friendGraph: [[Int]] = [[Int]](repeating: [], count: n)
var isAvailable: Bool = false
for _ in 0..<m {
let friend = readLine()!.split(separator: " ").map({Int(String($0))!})
friendGraph[friend[0]].append(friend[1])
friendGraph[friend[1]].append(friend[0])
}
var checked: [Bool] = [Bool](repeating: false, count: n)
func dfs(_ now: Int, level: Int) {
if isAvailable {
return
}
if level == 4 {
isAvailable = true
return
}
checked[now] = true
for i in 0..<friendGraph[now].count {
let friend = friendGraph[now][i]
if !checked[friend] {
checked[friend] = true
dfs(friend, level: level + 1)
if isAvailable {
return
}
checked[friend] = false
}
}
checked[now] = false
}
for i in 0..<n {
dfs(i, level: 0)
if isAvailable {
break
}
}
if isAvailable {
print(1)
} else {
print(0)
}
}
solution()'Algorithm > BaekJoon' 카테고리의 다른 글
| [백준] 14226번 - 이모티콘 [Swift] (0) | 2021.04.04 |
|---|---|
| [백준] 5014번: 스타트링크 [Swift] (0) | 2021.03.15 |
| [백준] 2644번: 촌수계산 [Swift] (0) | 2021.01.12 |
| [백준] 7562번 나이트의 이동 [Swift] (0) | 2021.01.07 |
| [백준] 9205번 맥주 마시면서 걸어가기 [Swift] (0) | 2020.12.27 |
- Total
- Today
- Yesterday
- System
- 코딩테스트
- Combine
- 프로그래밍
- 코테
- IOS
- operating
- Apple
- 백준
- 문법
- 알고리즘
- mac
- document
- dfs
- Publisher
- Xcode
- Swift
- pattern
- BFS
- design
- DP
- OSTEP
- 테이블뷰
- 아이폰
- 스위프트
- 동시성
- 자료구조
- OS
- operator
- 앱개발
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
