티스토리 뷰
문제 링크
Unique Paths - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Example 1:
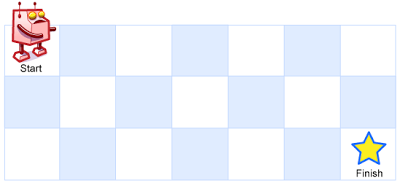
Input: m = 3, n = 7 Output: 28
Example 2:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Down -> Down 2. Down -> Down -> Right 3. Down -> Right -> Down
Example 3:
Input: m = 7, n = 3 Output: 28
Example 4:
Input: m = 3, n = 3 Output: 6
Constraints:
- 1 <= m, n <= 100
- It's guaranteed that the answer will be less than or equal to 2 * 109.
문제 풀이
이 문제는 그림과 같이 주어진 체스판? 같은 곳에서 한 번에 상하좌우로 한 칸씩 이동하는 로봇이 (0,0)에서 (m-1,n-1)로 가는 모든 방법의 수를 구하는 문제입니다.
제일 처음 문제를 보고 생각난 풀이법은 DFS, BFS였고 실제로 그렇게 풀다가 발견한 조건 중 정답이 2억 미만이어야 한다는 조건을 보고 이 문제가 그렇게 풀면 시간초과가 발생한다고 느껴서 DP로 접근했습니다.
DP로 접근 중 발견한 규칙은 아래와 같습니다.
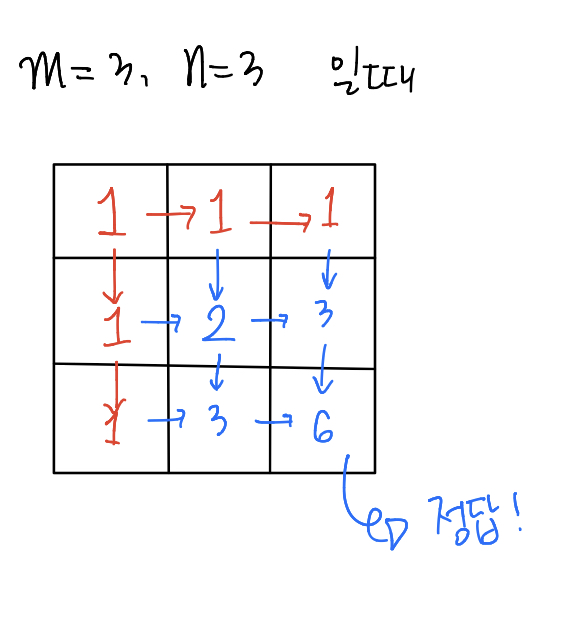
위의 그림과 같이 2차원 배열에서 위와 왼쪽을 더한 합이 그 위치의 값이 되는 거에요.
정확히 말하자면 해당 위치로 갈 수 있는 모든 방법의 수입니다.
따라서 위와 같이 주어진 m,n값으로 2차원 배열을 만들어서 계속 더해주기만 한 뒤 (m-1,n-1) 위치의 값을 정답으로 반환만 해주시면 됩니다. 아! 그리고 이 문제는 정답이 2억보다 크면 모두 2억을 반환하는 조건이 있으므로 그거도 처리해줘야해요.
안하면 범위 초과 문제가 발생합니다 ㅎㅎ;;
감사합니다.

소스 코드
class Solution {
func uniquePaths(_ m: Int, _ n: Int) -> Int {
var result: [[Int]] = [[Int]](repeating: [Int](repeating: 0, count: n), count: m)
for i in 0..<m {
for j in 0..<n {
if i == 0 || j == 0 {
result[i][j] = 1
} else {
result[i][j] = min(result[i-1][j] + result[i][j-1], 2000000000)
}
}
}
return result[m-1][n-1]
}
}'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode] 48번 - Rotate Image [Swift] (0) | 2021.02.04 |
|---|---|
| [LeetCode] 64번 - Minimum Path Sum [Swift] (0) | 2021.02.01 |
| [LeetCode] 56번 - Merge Intervals [Swift] (0) | 2021.02.01 |
| [LeetCode] 46번 - Permutations [Swift] (0) | 2021.01.27 |
| [LeetCode] 39번 - Combination Sum [Swift] (0) | 2021.01.27 |
- Total
- Today
- Yesterday
- 테이블뷰
- 코테
- DP
- 알고리즘
- Swift
- 동시성
- Combine
- System
- document
- OSTEP
- OS
- operating
- 코딩테스트
- Xcode
- 자료구조
- IOS
- mac
- 아이폰
- 스위프트
- operator
- pattern
- Apple
- Publisher
- 백준
- 문법
- design
- BFS
- 프로그래밍
- dfs
- 앱개발
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
